EDIT 2022:
Just use Jan’s calculator:
Run it for your bikes and write the pressure on the tires or the rims.
Ignore all this old stuff:
Here’s a short overview of tire pressure on the Problem Solver’s blog. It’s a little more concise than this page, and has more pictures.
The Calculator
The pressure calculator was created by Dave Adams, who sent it to me because of a tire pressure post I’d put up with an extended chart. You can open the spreadsheet in Open Office, Excel, or Google Docs and use it for free. Just remember “Dave Adams” when you use it.
How to Use It
Fill in the yellow fields in the spreadsheet (tire width; bike and rider weight; percent of weight on each tire). Go pump your tires. You can make (copy) a tab for each of your bikes, and make the tires and rider fatter or thinner over time (or adjust for touring loads).
The Science
According to Frank Berto and Jan Heine (of Bicycle Quarterly magazine), two top bicycle science guys, the most efficient bicycle tire pressure is one that gives you a 15% drop in tire height when you get on the bike. “This tire has too little air!” It’s squishy and hard to turn. “This tire has too MUCH air!” It loses energy bouncing off small surface irregularities. “This tire is JUST RIGHT!” Fifteen percent is the Mama Bear of tire drop.
Given that you want each tire to ‘drop’ 15%, and bikes don’t weight the front as much as the rear, you don’ t want the same amount of air in each tire. It seems obvious when you think about it, but it was revelation to me.
Most bikes put 60% of the weight on the rear, for a 40-60 fore-aft weight distribution. The “Quickbeam” tab in the spreadsheet is set up this way, and I actually weighed the bike with me on it to get the split. I could have saved some work and trusted to Bicycle Quarterly, but I like to check things for myself.
Low-trail French Randonneuring bikes are different, with only 55% on the rear. The “Ross” tab in the spreadsheet is for my low-trail Ross Super Grand Tour fixed gear tourer. Also weighed out accurately to confirm the BQ numbers.
Dave says his equation looks like this:
PSI = 153.6 * Weight / (TireSize^1.5785) – 7.1685
History
A few years ago, in the Spring of 2007, Bicycle Quarterly had a “Tire Drop” article based on Frank Berto’s research about proper inflation for best efficiency, in which they published a very useful graph, and instructions on how to set up your tires.
It didn’t have a line for 35mm tires, which I used at the time, so I added another line, and extended it to allow for heavy loads. Jan Heine gave me permission to republish the Bicycle Quarterly graph with my additions, and it turned out to be pretty useful for some people. I actually had an internet friend send it to me, not knowing I’d posted it in the first place.
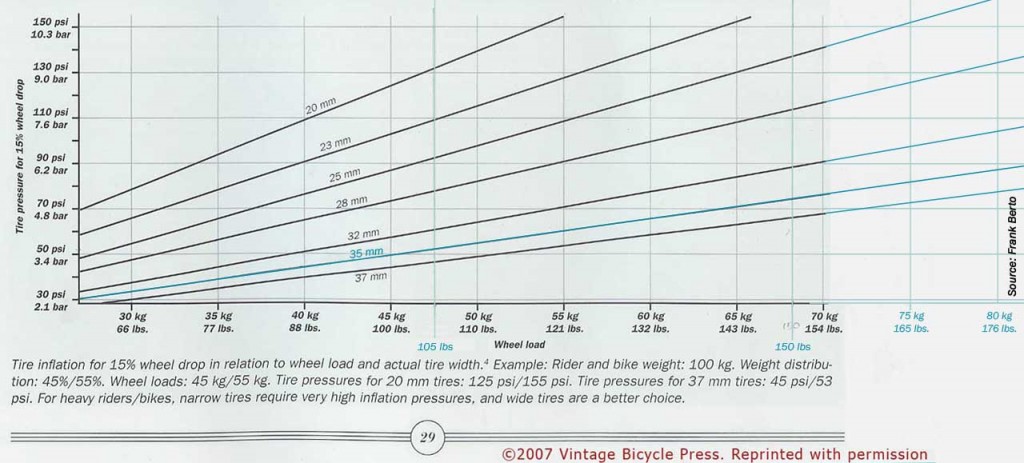 Dave Adams saw the post in his research on the same subject, and sent me a copy of his spreadsheet, which I’ve been using ever since. With his permission, I posted it to the RBW (Rivendell Bicycle Works) Google Group, where it’s also archived.
Dave Adams saw the post in his research on the same subject, and sent me a copy of his spreadsheet, which I’ve been using ever since. With his permission, I posted it to the RBW (Rivendell Bicycle Works) Google Group, where it’s also archived.

Thanks for this. Coincidentally, I’d just been re-reading the BQ article before coming here. Will adjust pressures tomorrow morning before heading out…
I should re-read the article again, too. I hope Jan publishes something more. I believe he has been working with Berto’s raw data, and I think he may be trying to factor in sidewall stiffness. That’s just a guess, though. Stiffer tires seem to feel better to me at a slightly lower pressure, but I haven’t done any empirical tests.
Hi,
I made a French open document version (weight in kilos and pressure in bars) : http://l0z.free.fr/velo/pression-pneu-ideale-ISO.ods
Thank you for your sharing your work,
loz
Thanks for the great explanation and tools. LOVE the spreadsheet that does all the work for me.
The “just right” belongs to the Baby, Bear, though–not the Mama Bear. (oatmeal too hot; too cold; just right/chair too big; too small; just right/bed too big; too small; just right)
Hi Elizabeth,
If we are being pedantic its bed too hard / too soft.
Hi Dave,
In my case it’s most always both, too soft and too short, lol.
“
That’s what SHE said!” :^)I wonder how much pressure one would need for the same width tyres but in size 26″.
10%, 15% more?…
Hi Barteos,
It looks like 10% is the right answer. I’m surprised it’s that much, and hence surprised it’s not a variable in the spreadsheet. Apparently calculating the volume of a torus is really complicated, so when I did this a long time ago, I just pretended they were cylinders.
Today, I just went to this online torus calculator, and calculated the volume of a 700c and a 26″ 45mm tire.
After microliter to liter conversion, it came to 2.9 liters vs 3.1 liters, which looks like ~10% to me.
Many thanks :-)
Don’t be surprised tire size is not a variable. The equation was derived from Berto’s measured points. There were none for other sized wheels.
You’ll note that even with just the 700c this needed a non-linear factor. It was fortuitous that each tire size seemed to have a linear relationship between weight and pressure. The non-linear factor accounted for factors in play between different tire sizes.
That non-linear factor MIGHT be OK for different wheel sizes, but I have a nagging suspicion that varying wheel size would yet another non-linear component to account for a brand new set of torus shapes. Sure would be nice to have a collection of similar runs for 26″ tires.. and 650B. THEN we could take the same successive approximation approach.
THAT data would be a nice feed in to the Eureqa tool available at Cornell :)
Thanks, Dave! The great part of the spreadsheet is that I don’t have to really get the math! I just kind of spitball another 10% off on my 26″ tires. When I remember. Otherwise I just air ’em up to the numbers.
Philip,
Doing the Maths the 26″ tyre should be about 15% higher pressure than the 700C, if you spitball another 10% off you will actually be under inflating the tyres by 25% compared to what is suggested to get that magic 15% drop.
Hey I was wondering what numbers you did math on? For a 559mm 26in tire, it’s 10.1 percent less area than a 622m 700c tire. Since width is already accounted for I just subtracted the area to get the 10% that I added that to the suggested psi
According to my handy reference, Engineering Formulas (Gieck & Gieck), the volume of a torus is simply (PI^2)/4 * D * d, where d is the diameter corresponding to tire width, and D is the diameter of a circle around the center of the torus (basically average of ID and OD.)
Oops, make that (PI^2)/4 * D * d^2
All the art majors in the room raise their hands. Actually that looks fairly simple. The “pretend it’s a cylinder” method did its job, though. It showed that the difference in circumference (“length”) was an order of magnitude less (“way less”) than the difference in diameter (“diameter”).
Hey, Dave, I just looked at Cornell’s Eureqa tool… WHOA!
That just sounds like magic.
Modelling equations to data is a risky business, great fun but can be very misleading. Best done semi manually so you understand the limitations of your model and have awareness that, though the one you have produced might be the simplest best fit to the data you have, there are many others that might be statistically acceptable and possibly better reflect underlying mechanisms that are producing the data.
What variable(s) would need to be changed to calculate for smaller wheel sizes?
I use 559 on the back and 406 on the front, and there are many other permutations that are commonplace.
I would expect this to be of most use for people with unusual tyre sizes, as the more common ones can usually be arrived at simply by experience of others.
If I relied on the experience of others, I’d ride 25mm tires aired up to the number on the sidewall, and still be underinflating the rear…
Dave indicates that to make a formula for each smaller wheel size, you’d need to measure the pressure it takes to get the 15% drop at a bunch of different weights, then use that to make a formula that works for that size.
In the article from BQ it states:
“Berto measured this for 700C tires, but the values apply to other tire sizes as well.”
This makes sense when you think we are dealing with PSI, which cause the size of the contact area.
I’ve come across this treatment of optimum tire pressure based on Berto’s work on several websites. What I haven’t seen is anybody point out that for 23mm wide tires, the calculated optimum tire pressure in psi is essentially the same as the wheel load in lbs, within 5% for wheel loads between 53-198 lbs (<2% between 67-104 lbs). Outside of these ranges, decrease the pressure a couple psi for light wheel loads (or don't, since the difference between the optimal 36 psi and 40 psi for a 40 lb wheel load is likely not an issue, and your pressure gauge likely reads high anyway), and increase the pressure a few psi for heavy loads (or don't, since the tire is possibly being overloaded and you should consider getting a wider one instead).
This makes for a handy rule of thumb for riders of 23mm tires: PSI=LOAD !!!
Shouldn’t the pressure per square inch should exactly match the tire load in lbs when the tire is 25.4mm wide? i.e. 1″? It doesn’t seem to, though.
PSI will equal wheel load when the developed contact patch is 1 square inch (not necessarily 1 inch wide), neglecting tire stiffness. So for the 23mm wide tire, it simply means the contact patch is ~1 square inch at 15% drop. For a wider tire at the same drop, you would expect a larger contact patch, and thus a lower psi.
BTW, I agree that most of the mfr’s info on the sidewall is not to be trusted, but it would be a Bad Idea ™ to exceed the maximum recommended pressure on a tire by more than about 10%. If in doubt, see also the mfr’s spec sheet for the tire in the box or on their website (but make sure you’re looking at the right model/size/version/flavor!).
Bad Idea™ indeed! My preference is for going fat, and keeping the PSI under 80. If your bike doesn’t handle a fatter tire, there are many that do, from Rivendell, Surly, Jones, and Black Mountain, without getting into custom (*cough* Winter, MAP, Potts). Some people also put 650B wheels on 700C road frames to run 32-42mm tires. I’ve never done it, but I like it in every way.
Great stuff Philip! However, the google doc seems to be ravaged by users. Can you upload a clean, locked down version that people could just download or copy to edit?
Hi Darren,
I’ll try to upload a clean download copy for you this weekend, but Maker Faire is going to take up all Saturday.
I gave up on the Google doc a few months ago. People are just terrible. :^)
Hi Darren, sorry for the months-long delay!
Here’s a clean XLS file you can download for your own use: https://www.biketinker.com/wp-content/uploads/2011/04/Tire-Pressure-salvaged-doc.xlsx
Philip
All this is very good, and I for one appreciate the think time that went into the original work as well as the commentary that followed. Don’t know if anyone will every see this due to blog being 4 years old, but a consideration needs to be given to weight loading tires when riding – the practical end game is when you are going up a steep climb (weight shift to rear)or descending a steep mountain pass and having to make sharp corners (extreme loading of front). These worse case scenarios are what the tires really need to be pressured up for… Darryl
Hi Darryl, this post is actually… TEN years old! I’m sorry it took 6 months to get to the comments. Last comments were four years ago. :)
I agree with you. I run same pressures front and rear, mostly. I only check in with the calculators occasionally to make sure my ‘ballpark’ pressures are still in the ballpark.
I just don’t care that much about ‘best’ pressure anymore. It doesn’t seem to matter that much with nice tires, and if you’re running crap tires… it doesn’t matter that much either.